Determinar las cabeceras de una tabla donde tenemos los valores buscados

En el artículo anterior, vimos un ejemplo un poco rebuscado, para determinar en qué columnas (A, B, C…) se encontraban una serie de valores que teníamos en una tabla. La utilidad de ese ejercicio era poca, para qué negarlo :-( pero fue un reto interesante, para saber hasta qué punto Excel puede convertirse en una herramienta a medida, en la que podemos implementar funciones que no vienen de forma nativa dentro de la aplicación.

Ahora veremos algo más interesante, y que probablemente alguna vez hayáis necesitado, y si no ha sido así, seguramente en alguna ocasión necesitaréis. Se trata de obtener los rótulos o cabeceras de una tabla, donde tenemos los valores que estamos buscando. Como siempre, lo veremos con un sencillo ejemplo. Imaginemos que tenemos tres zonas donde nuestra empresa vende: la zona A, la zona B, y la zona C. Las ventas las tenemos divididas en meses, de enero a diciembre, y pretendemos determinar qué mes es aquel que tiene las ventas máximas en cada zona. La tabla sería la siguiente:

Si nos fijamos bien, las ventas máximas de la zona A, son 78, y se producen en el mes de octubre. Pues precisamente eso, obtener el mes de octubre, es lo que pretendemos conseguir que nos determine Excel.

Como bien sabéis, obtener la cifra máxima de ventas para la zona A, sería tan sencillo, como poner esta fórmula:

=MAX(C5:N5)

Pero la pregunta es: ¿cómo hacemos para que Excel nos diga que ese valor máximo que obtenemos en la zona A, y que corresponde a unas ventas de 78, se producen en el mes de octubre (OCT)?. Pues de una forma bastante sencilla. Solo tendremos que utilizar la función MAX, para determinar el valor máximo de ventas.

También utilizaremos la función COINCIDIR que nos determinará el número de columna en la que tenemos el valor máximo, teniendo en cuenta que el número de la columna se determina en función del rango que escojamos, y tomando como columna inicial, aquella que corresponda a la primera celda del rango. ¿Esto último parece complicado?. No, no lo es. Si te digo que escogemos como rango de la zona A, el que va desde C5 hasta N5, la columna C sería la primera, y la columna N sería la duodécima. Con esta función, obtendremos que la columna cuyas ventas son máximas en la zona A, se corresponde con la número diez.

Y por último, necesitaremos convertir esa columna número diez, en la cabecera o rótulo correspondiente de la tabla, es decir, en OCT (mes de octubre). Para ello, nos bastará con utilizar la función INDICE.

Sería algo tan sencillo, como aplicar esta fórmula, para determinar el mes en el que se producen las ventas máximas de la zona A:

=INDICE(C4:N4;COINCIDIR(MAX(C5:N5);C5:N5;0))

Para obtener lo mismo de la zona B, sería esto:

=INDICE(C4:N4;COINCIDIR(MAX(C6:N6);C6:N6;0))

Y en la zona C, las ventas máximas se producen en el mes que nos devuelve como resultado esta fórmula:

=INDICE(C4:N4;COINCIDIR(MAX(C7:N7);C7:N7;0))

Y en esta imagen, podéis ver los resultados:

Desde aquí, podéis descargar el libro de Excel, con el ejemplo que hemos visto en este artículo.

33 Utilidades para Microsoft Excel

Hoy os presento un manual en pdf, de lo que creo que podrían ser, las 33 mejores utilidades para Microsoft Excel que he publicado en el blog. Quizás algunos de vosotros no estéis de acuerdo, y penséis que hay otros artículos en el blog que deberían incluirse en el manual. Muy probablemente tengáis razón, pero he escogido esas 33 utilidades, después de hacer muchos descartes.

Este manual con 33 utilidades para Microsoft Excel, no pretende ser un manual de cabecera, pero si un manual de consulta, especialmente ideado para aquellos lectores que quieran aprender las posibilidades de las macros en Excel. No obstante, este manual no solo incluye macros, sino que también podréis encontrar en él, funciones propias de Excel, como la TIR, y el VAN, por poner solo dos ejemplos.

El manual, como todo lo que encontrarás en este humilde blog de Excel, es gratuito y de libre distribución, por lo que puedes imprimirlo, enviárselo a tus amigos, compartirlo, y en definitiva, hacer lo que quieras con el :-)

En muchos de los artículos, podréis comprobar que al final de los mismos, hay un enlace para descargar un fichero con todo lo explicado, para que el usuario no tenga que partir de cero escribiendo el código fuente en Excel. Asimismo, se incluye un enlace a la entrada original de este blog, por si en algún momento el lector quiere acercarse hasta aquí, para ver si he realizado algún cambio o modificación en algún artículo del blog, como ha ocurrido recientemente por ejemplo, en el que explico como obtener datos de una página web.

Estas son las utilidades que he incluido en el pdf:

1. Obtener el nombre del archivo.
2. Obtener el nombre de la hoja.
3. Obtener la ruta, el nombre del fichero, y la hoja.
4. Mi primer macro en Excel.
5. Mi primer UserForm.
6. Introducir datos utilizando un formulario.
7. Modificar datos utilizando un formulario.
8. Mi primer ComboBox.
9. Sacándoles provecho a los ComboBox.
10. Macro al abrir o cerrar un libro.
11. Desproteger una hoja de cálculo.
12. Crear carpetas (o directorios), desde Excel.
13. Poner la hora en una celda.
14. Crear hojas con un clic.
15. Buscar hojas ocultas.
16. Mostrar y ocultar hojas, utilizando macros.
17. Leer una base de datos Access.
18. Simultanear filas de colores.
19. Validación con datos en otra hoja.
20. Validación de listas dependientes.
21. Control horario: horas normales y horas extras.
22. Números aleatorios no repetidos.
23. Préstamos y cálculo de hipotecas.
24. Préstamos según el método americano.
25. Préstamos con amortización de capital constante.
26. Calcular la TAE.
27. Calcular la TIR y el VAN.
28. Evolución de un capital a interés simple e interés compuesto.
29. Calcular la letra del NIF/DNI.
30. Controlar vencimientos de facturas y recibos.
31. Calcular vencimientos.
32. Obtener datos de una página web.
33. Calendarios para imprimir.

Aquí os dejo una imagen de una vista a 4 páginas, para que os hagáis una idea de lo que podéis encontrar en el pdf que podéis descargar más abajo:


Ya no os hago esperar más. Aquí tenéis el manual con las 33 utilidades para Microsoft Excel (cliquead en la imagen para descargar el manual en pdf):

Si te ha gustado este manual en pdf, te agradecería que dejases un comentario.

Buscar valores en un rango de datos

Hace poco, recibíamos una consulta de un usuario en nuestra página de facebook, en la que nos preguntaba como localizar determinados valores en un rango de datos. Concretamente, lo necesitaba para determinar la tarifa aplicable por un servicio de transporte o mensajería, en función del peso del envío.

Vamos a ver como resolver tan interesante cuestión. Para ello, como siempre, ilustraremos la explicación con un sencillo ejemplo. Supongamos que tenemos la siguiente tarifa de transportes, para las localidades que se indican en la tabla adjunta:


Supongamos ahora, que queremos saber cuanto nos costaría enviar un paquete que pesa 70 kgs. a Sevilla. Visualmente, lo tenemos fácil, pues en la tabla tenemos que localizar la fila correspondiente a los 70 kgs. y la columna correspondiente a Sevilla. Eso nos dará como resultado, que el precio de ese transporte es de 94,00 euros, dólares, pesos, o cualquier otra unidad monetaria con la que trabajemos. Pero claro, queremos obtener ese dato, de forma automática, simplemente informando en algún sitio, del destino de la mercancía, y del peso.

Para ello, montaremos esta plantilla de Excel, donde a través de dos listas de validación, podremos seleccionar el destino y el peso del producto, y una vez seleccionados estos datos, debajo nos aparecerá el importe del envío.


Para calcular el precio, todo es muy sencillo, con esta fórmula:

=SUMAPRODUCTO((B6:B15=D21)*(C5:F5=D20)*(C6:F15))

Esta fórmula, lo que viene a hacer es buscar en el rango de celdas comprendido entre B6 y B15, el dato informado en la lista de validación de D21, es decir, el peso del paquete que enviaremos. Seguidamente, nos busca en el rango de C5 a F5, la localidad informada en la lista desplegable de la celda D20. Y por último, con esos dos datos, lo que hace la fórmula es localizar el importe en el que confluyen ambos datos (peso y localidad), dentro del rango comprendido entre C6 y F15. Como veis, no es nada complicado.

También obtendremos el mismo resultado, si utilizamos las funciones INDICE y COINCIDIR, en lugar de SUMAPRODUCTO, de la siguiente forma:

=INDICE(C6:F15;COINCIDIR(D21;B6:B15;0);COINCIDIR(D20;C5:F5;0))

En este caso, la fórmula la leeríamos más o menos así:

Busca en la matriz de datos que hay entre C6 y F15, la fila cuyo número es el resultado de aplicar la función COINCIDIR(D21;B6:B15;0), y cuya columna es el resultado de aplicar la función COINCIDIR(D20;C5:F5;0).

COINCIDIR(D21;B6:B15;0) nos indica que posición ocupa en valor de la celda D21, dentro del rango de datos comprendido entre B6 y B15. Una lectura similar se podría hacer de COINCIDIR(D20;C5:F5;0), pues nos indica la posición que ocupa el dato de D20, dentro del rango de datos comprendido entre C5 y F5.

Esto puede parecer algo complicadillo, pero si lo imprimís y lo leéis de nuevo, teniendo la hoja de cálculo de Excel delante (la que podéis descargar al final de este artículo), os será mucho más fácil de “digerir”.

Esta segunda opción donde utilizamos las funciones INDICE y COINCIDIR, nos sería especialmente de utilidad, en el caso de tener datos de texto en la matriz, en lugar de importes, pues la función SUMAPRODUCTO nos daría error, al no tener datos numéricos.

Para hacerlo más elegante, en el ejemplo que podrás descargarte al final de este artículo, hemos puesto un formato condicional a las celdas, para que nos coloree de azul la celda con la tarifa, tal y como se muestra en el siguiente ejemplo:


A este tipo de localización de datos dentro de un rango de datos (o una matriz de datos), lo vamos a llamar localizar datos en una matriz, con datos de entrada exactos. Es decir, introduciremos los datos exactos de la localidad y sobretodo el peso del producto a enviar, para localizar el valor en la tabla. De hecho ya habíamos visto alguna que otra utilidad para localizar datos dentro de una tabla, utilizando algunos ejemplos de funciones personalizadas de bases de datos por aquí, y más funciones personalizadas de bases de datos, por este otro lado.

Llegados a este punto, nos encontramos con que la realidad del día a día es bien distinta, pues ese tipo de tarifas no suelen proporcionárnoslo así los transportistas de paquetería. ¿Verdad que cuando enviamos un producto, la tarifa de transportista nos informa de un peso por tramos?. Es decir, el transportista nos cobra en función de si el peso está dentro de un rango (o baremo) de pesos. Por eso, la tabla anterior no nos vale, y el más claro ejemplo es el siguiente: ¿cuánto nos costaría enviar 45,46 kgs. a Sevilla?. Pues siendo estrictos, a la vista de esa tabla anterior, no lo sabemos, pues no aparece ese peso en la tarifa.

Para solucionar esto, vamos a imaginar que la tarifa del transportista es esta otra:


En este caso, ya vemos que la cosa es mucho más realista, pues el transportista, nos va a ofrecer un precio, para un rango determinado de pesos, a cada localidad. En el ejemplo, podemos ver como la empresa de transportes nos va a cobrar 93 euros, dólares, pesos, o cualquier otra unidad monetaria con la que trabajemos, si llevamos entre 60,01 kgs. y 70 kgs., a Madrid. Es decir, si solicitamos que la empresa de paquetería nos lleve un paquete a Madrid, que pesa 62 kgs., nos cobrará lo mismo que si nos lleva 68 kgs.

A este tipo de localización de datos dentro de un rango de datos (o una matriz de datos), lo vamos a llamar localizar datos en una matriz, con datos de entrada dentro de un rango de datos.

Para localizar la tarifa correspondiente a un envío de determinado peso a una localidad, montaremos una tabla como esta, donde la localidad será una lista de validación, y el peso lo introduciremos manualmente:


Para calcular el precio, solo nos quedará aplicar esta fórmula:

=DESREF(C5;COINCIDIR(D21;B6:B15);COINCIDIR(D20;D5:G5))

¿Cómo se lee esta formulita?. Pues de una forma no muy complicada. Las funciones COINCIDIR ya las hemos explicado unos párrafos más arriba, y nos indican tanto la fila donde está el peso seleccionado, y la columna donde está la localidad elegida. La función DESREF, simplemente nos desplaza tantas filas y columnas como nos indican las funciones COINCIDIR, partiendo desde la celda C5.

Como veis, tenemos una forma bastante sencilla para localizar valores en una tabla, tanto, si se trata de valores exactos, como si se trata de valores dentro de un rango.

Desde aquí podéis descargar el fichero de Excel, con todo lo que hemos visto en este artículo.

Medias ponderadas

Hoy os presento un artículo, que aunque no es estrictamente algo que podamos considerar como puramente de Excel, creo que le va a servir a muchos usuarios que utilizan esta popular hoja de cálculo. Se trata de obtener lo que se denomina media ponderada.

La Real Academia Española (RAE), define la media ponderada como el "resultado de multiplicar cada uno de los números de un conjunto por un valor particular llamado su peso, sumar las cantidades así obtenidas, y dividir esa suma por la suma de todos los pesos".

¿Está claro, verdad?. Jajajaja. Probablemente leído así a bote pronto, esa definición lo que hace es confundir más que aclarar, pero si lo vemos con un ejemplo, nos daremos cuenta que es algo bastante sencillo de entender.

Vamos a suponer que hoy día 26-01-2011, efectuamos dos inversiones, una que nos rinde el 7% de interés nominal anual, y cuyo vencimiento es el 31-12-2011, y otra que rinde el 1% de interés nominal anual, y cuyo vencimiento es dentro de 5 días, es decir, el 31-01-2011. En ambos casos, supondremos que los intereses nos los retribuyen al vencimiento de cada inversión.

Si pasáramos esta información a nuestra hoja de cálculo de Excel, nos quedaría algo así:


Si alguien nos preguntara, a qué tipo de interés medio nos retribuyen la inversión, podríamos contestarle dos cosas:

a) Al 4,00% de interés medio, pues esa cifra resulta de hacer la meda de tipos de interés: (7%+1%)/2
b) Nos faltan datos para poder dar una respuesta.

Si hemos elegido al respuesta a), sin duda estaremos cometiendo un grave error, porque entre otras cosas, las dos inversiones no tienen el mismo vencimiento. Piensa por un momento que la inversión 1 vence dentro de 339 días, es decir, todavía queda mucho, mientras que la inversión 2 está prácticamente finalizada, por lo que debemos valorar esta circunstancia, para calcular el tipo medio de interés de nuestras inversiones, pues en caso de no hacerlo, estaremos ponderando más de la cuenta el tipo de interés de la inversión 2 (la que está a punto de finalizar). Llegados a este punto, podríamos reformular nuestro esquema en Excel, de la siguiente forma:


Si nos volvieran a preguntar cual es el tipo de interés medio al que retribuyen nuestras inversiones, la respuesta que podríamos dar, sería una de estas:

a) Al 6,91% de interés medio, pues esa cifra resulta de multiplicar el 7% por los días que quedan hasta el vencimiento de esta primera inversión, es decir 339 días, multiplicando nuevamente el 1% por los días que quedan hasta el vencimiento de esta segunda inversión, es decir, 5 días, y dividiendo todo ello entre la suma de 339 y 5. Es decir, ese tipo medio del 6,91% lo obtendríamos de la siguiente fórmula:


b) Nos faltan datos para poder dar una respuesta.

Como en el caso anterior, si hubiésemos dado como respuesta la a), estaríamos cometiendo un error, pues nos falta el último dato, el importe de cada una de las inversiones (la inversión 1, y la inversión 2), y que es condición necesaria para poder determinar el tipo de interés medio al cual nos retribuyen esas inversiones. En ningún momento hemos dicho que ambas inversiones sean del mismo importe, por eso presuponer ese dato sería un error.

Vamos a suponer que la inversión 1 es de 10.000 euros, y que la inversión 2 es de 5.000 euros. Reformulemos por tanto nuestro esquema en Excel, para tenerlo todo más claro, de un vistazo:


Si ahora nos hicieran la preguntita de marras, nuestra respuesta sería que el tipo de interés medio resultante de estas inversiones, es del 6,96%, pues lo obtenemos de resolver la siguiente fórmula:


En realidad, lo que estamos haciendo, es ponderar (sopesar, o medir de forma proporcional) cada tipo de interés, con respecto al importe de cada una de las inversiones, y con respecto a la fecha de cada uno de los vencimientos. En términos matemáticos, lo que hemos hecho no es más que ponderar la media, o como reza el título de este artículo, calcular la media ponderada.

Si volvemos a mirar esta última fórmula donde obtenemos ese 6,96% de interés medio (ponderado), y releemos nuevamente la definición que da la RAE sobre la media ponderada, estoy seguro que ahora tendremos las cosas mucho más claras, y habremos entendido esta definición.

Como colofón de este artículo, vamos a suponer ahora que tenemos 20 inversiones, en lugar de 2, como era el caso que contemplábamos en el ejemplo. En ese caso, en lugar de hacer una fórmula donde el numerador y el denominador van a ser larguísimos, podemos solucionarlo muy fácilmente con el uso de la función SUMAPRODUCTO. Vamos a verlo con un ejemplo, donde podemos contemplar en la imagen, la fórmula que aparece en la barra de fórmulas:


Podemos construir dos columnas auxiliares, pare ver que efectivamente, la función SUMAPRODUCTO nos arroja el mismo resultado, que una fórmula tradicional:


En realidad, la fórmula SUMAPRODUCTO, lo que va a hacer es multiplicar cada elemento de las matrices que le indiquemos, sumando cada una de las líneas, de tal forma que si por ejemplo ponemos esto:

=SUMAPRODUCTO(C5:C24;E5:E24;F5:F24)

...le estaremos diciendo que haga esto:

=(C5*E5*F5)+(C6*E6*F6)+(C7*E7*F7)+(C8*E8*F8)+(C9*E9*F9)+(C10*E10*F10)+(C11*E11*F11)+(C12*E12*F12)+(C13*E13*F13)+(C14*E14*F14)+(C15*E15*F15)+(C16*E16*F16)+(C17*E17*F17)+(C18*E18*F18)+(C19*E19*F19)+(C20*E20*F20)+(C21*E21*F21)+(C22*E22*F22)+(C23*E23*F23)+(C24*E24*F24)

Es decir, tanto la función SUMAPRODUCTO que hemos puesto, y esta otra fórmula tradicional tan larga que acabamos de poner, hacen exactamente lo mismo.

Espero que os haya sido útil este artículo, y que lo podáis aplicar alguna vez en vuestro trabajo. Como siempre, desde aquí podéis descargar el fichero de Excel, con el ejemplo final que hemos visto en este artículo.

Calcular vencimientos

En el artículo anterior, donde os dejé una aplicación para controlar vencimientos de facturas y de recibos, más de uno os habréis dado cuenta de que en una hoja, había una columna donde informábamos del vencimiento de las facturas. Esta columna utilizaba como referencias los nombres de celdas, con lo que intentar descifrar esa fórmula podía ser un trabajo de investigación (nada difícil, pero sí, más complicado de lo normal).

Para solucionar el asunto, vamos a ver ahora en este artículo, esa misma fórmula, pero sin utilizar los nombres de celdas.

Supongamos que tenemos los siguientes datos, en las siguientes celdas:

E5: Aquí tenemos el plazo de crédito a los clientes. Puede ser 30, 45, 60, 90 o los días que hayamos acordado.

E6: Aquí tenemos la fecha de pago fija del cliente. Hay clientes que para centralizar sus pagos en una fecha determinada, suelen pagar sus facturas un único día al mes. Puede ser el día 5, el día 10, el día 15, o cualquier otro día de pago fijo que tenga el cliente. Si nuestros clientes no tienen un día de pago fijo, dejaremos esta celda vacía (sin dato).

B8: Fecha de emisión de la factura.

Si queremos calcular el vencimiento de la factura, deberemos poner esta fórmula en la celda donde queramos informar este dato:

=SI($E$6<>"";SI(DIA(B8+$E$5)>$E$6;MIN(FECHA(AÑO(C8);MES(C8)+1;DIA($E$6));FIN.MES(B8+$E$5;1));MIN(FECHA(AÑO(C8);MES(C8);DIA($E$6));FIN.MES(B8+$E$5;0)));B8+$E$5)

Podemos ver una tabla con esa información, en la siguiente imagen (clic para ampliarla):


Si os fijáis en la tabla de la imagen anterior, la segunda columna muestra el vencimiento teórico, o vencimiento inicial, con independencia de que el cliente tenga o no, un día de pago fijo. En la tercera columna, vemos ya el efecto de desplazar ese vencimiento inicial, a aquel que le correspondería realmente, teniendo en cuenta el día de pago fijo que tiene el cliente. En la cuarta columna se muestran los días de vencimiento real contados desde la fecha de emisión de la factura.

Para que nos funcione la fórmula anterior, donde aparece la función FIN.MES, debemos tener habilitadas las "Herramientas para análisis", en Excel 2003 podemos hacerlo desde el menú Herramientas, seleccionando la opción de menú Complementos. En Excel 2007 deberemos pulsar el botón de Microsoft Office (arriba a la izquierda), seleccionaremos el botón de Opciones de Excel (situado en la parte inferior de la ventana que nos aparecerá), luego seleccionaremos Complementos, y a continuación nos situaremos encima de las Herramientas para análisis. Pulsaremos sobre el botón "Ir", y habilitaremos esta opción marcando la muesca correspondiente.

Si lo que necesitamos es algo más sencillo, como simplemente sumar unos días de vencimiento a una fecha, podemos hacerlo de esta otra forma, mucho más sencilla, tal y como se muestra en la imagen, donde sumamos 30 días a la fecha de factura:


Si os fijáis, en imagen anterior podemos ver que la celda C5 tenemos como fórmula, el valor de la celda C4, y le hemos sumado 30 días. Para que en esas dos celdas los datos nos aparezcan como en la imagen anterior, simplemente deberemos darle formato personalizado a las celdas, con formato dd-mm-aaaa.

Desde aquí podéis descargar el fichero de Excel, con el ejemplo que hemos visto en este artículo. En este fichero encontraréis una tabla con todos los días del año, y el vencimiento de las facturas en función del día de emisión de las mismas, teniendo en cuenta el plazo de crédito que concedamos al cliente, y la fecha de pago fija que tiene (si es que la tiene).

Calcular la TAE

La TAE es la tasa anual equivalente, o también llamada, tasa anual efectiva. Lo que realmente nos interesa, es saber que significa eso, y como se calcula.

Antes de entrar en materia, comentaros que os dejo una mini aplicación que os permitirá calcular la TAE de una operación financiera, con intereses pagaderos al vencimiento. Tan solo tendréis que informar el tipo de interés nominal, y el plazo de pago de los intereses:



En un artículo anterior ya hablamos sobre el cálculo de la TIR con Solver, así que gran parte de lo que aquí explicaremos, lo podéis ampliar con la información contenida allí, aunque en principio no será necesario. También podéis ver el uso de la TAE en una operación financiera como es el caso de un contrato de préstamo, pues en el artículo donde colgué la plantilla para el cálculo de préstamos, está incorporada esta función.

Vamos a explicar qué es la TAE con un sencillo ejemplo. Imaginemos que disponemos de 5.000 euros, y queremos invertirlos en un depósito a plazo fijo a un año, pero tenemos dos opciones:

• El Banco A nos ofrece un tipo de interés nominal del 7% anual, pagadero al vencimiento.


• El Banco B nos ofrece un tipo de interés nominal del 6,95% anual, pagadero mensualmente.

Así a bote pronto, podemos pensar que la opción que nos plantea el Banco A, es más interesante, porque nos da 350 euros al cabo de ese año (5.000 x 0,07), mientras que el Banco B nos da solamente 347,50 euros (5.000 x 0,0695). Es decir, el Banco A nos da 2,50 euros más de intereses al año (350 – 347,50).

Desde un punto de vista financiero, nuestro objetivo es siempre maximizar el beneficio procedente de una inversión, por lo que hay que analizar la rentabilidad efectiva de ambas operaciones que nos plantean los bancos, antes de decidirnos. Vamos a ver como analizar la rentabilidad efectiva, es decir, obtener la TAE de ambas operaciones.

Si el Banco A nos paga los intereses al vencimiento, lo que está claro, es que solo podremos disponer de ellos a la finalización del contrato que hemos firmado con el banco, es decir, al vencimiento del depósito (al cabo de ese año). El Banco B en cambio, nos paga cada mes los intereses, por lo que podemos disponer de ellos mensualmente. Esto implica que podemos retirar esas cantidades (los intereses mensuales) para gastarlos en lo que queramos, o mejor aún, para invertirlos nuevamente. Es aquí donde entra en juego el concepto de la TAE, pues el propio concepto de la TAE para lleva implícito que vamos a reinvertir esos intereses.

La opción del Banco A es muy clara, pues al cabo de un año, podremos retirar el capital inicialmente invertido (5.000 euros), más los intereses (350 euros). Es decir, al cabo de 1 año, dispondremos de 5.350 euros.

En cambio la opción del Banco B tenemos que analizarla con más detenimiento, pues nos pagan intereses cada mes. Para saber que intereses mensuales obtendremos, tenemos dos opciones:

• Podemos coger el tipo de interés nominal anual, dividirlo entre los 12 meses, y aplicar ese tipo de interés a los 5.000 euros: 0,0695 / 12 x 5.000 = 28,9583 euros de intereses mensuales.


• O también podemos calcularlo, aplicando a los 5.000 euros, el tipo de interés que nos da el Banco B, y dividiendo esos intereses totales, por 12, porque los cobraremos mensualmente: 5.000 x 0,0695 / 12 = 28,9583 euros mensuales.

Como habéis visto, ambas opciones para calcular los intereses mensuales son idénticas, porque matemáticamente son lo mismo.

Pero... ¿qué pasaría si esos intereses de 28,9583 que cobraríamos también al cabo de un mes, y los invirtiéramos al mismo tipo de interés del 6,95%, durante los 11 meses que nos quedan hasta finalizar el contrato del depósito a plazo fijo?. Esta pregunta es básica, y es la que tendríamos que hacernos siempre, para comprender el auténtico significado de la TAE.

Vamos a ver en una tabla de Excel, que pasaría, si los intereses que cobramos mensualmente con la opción del Banco B, los invertimos por el tiempo que reste hasta finalizar ese año, en el que recuperaríamos la inversión inicial de los 5.000 euros.


La columna bajo el título de "Capital invertido" incluye los 5.000 euros invertidos inicialmente, más los intereses que nos van pagando cada mes, y que también se reinvierten por el periodo que resta hasta finalizar la imposición. Por ejemplo, la recuperación del capital, más los intereses que nos pagan el primer mes, los podemos reinvertir durante 11 meses. La recuperación del capital, más los intereses que nos pagan al cabo del segundo mes, los podemos reinvertir durante 10 meses, y así sucesivamente, hasta que al final, cuando cobramos los intereses del mes nº 12, ya no podemos reinvertir nada nuevamente, porque ha finalizado el plazo de tiempo por el que abrimos el depósito a plazo fijo.

También podemos ilustrarlo con este otro ejemplo, donde más claramente se puede observar como reinvertimos los intereses:


Como veis, hemos conseguido 347,50 euros de intereses con la opción del Banco B, y reinvirtiéndolos, nos darían 11,29 euros adicionales, es decir, obtendríamos un total de 358,79 euros, si optimizásemos la inversión (reinvirtiendo los intereses). También hemos calculado la TAE de la operación, que no es más que dividir los intereses totales que obtendríamos (358,79 euros), entre el capital invertido (5.000 euros), porque es a un año, lo que nos da una TAE del 7,1757%.

Llegados a este punto, ya estamos en condiciones de saber que inversión es más rentable desde un punto de vista financiero (optimizando la inversión). El Banco A nos da unos intereses de 350 euros al año, mientras que con la opción del Banco B podemos obtener 358,79 euros.

En el caso del Banco A, el tipo de interés nominal del 7%, es también la TAE, porque no podemos reinvertir los intereses, ya que los obtenemos al final, cuando finaliza el depósito a plazo fijo. En el caso del Banco B, el tipo de interés nominal es del 6,95%, pero la TAE es del 7,1757%, lo cual desde un punto de vista financiero, nos deja las cosas muy claras: el Banco B es la mejor opción.

Como habéis visto, aunque aparentemente el Banco A inicialmente era la mejor opción, hemos demostrado que no es así, y que el Banco B nos ofrecía desde un punto de vista financiero, la mejor opción para maximizar nuestros beneficios (nuestros intereses).

Para calcular la TAE de una operación financiera, os dejo una hoja de cálculo para descargar, que os simplificará mucho la tarea, pues tan solo tenéis que introducir el tipo de interés nominal anual, y los periodos de pago al año (pagos semestrales, pagos trimestrales, pagos mensuales, etc.). Es la plantilla de Excel cuyas imágenes podéis ver al principio de este artículo.

Desde aquí podéis descargar los dos ficheros de Excel, comprimidos en formato zip, con los ejemplos que hemos visto en este artículo. En uno de ellos tenéis la tabla con el estudio de rentabilidad de la opción ofrecida por el Banco B (la tabla de la última imagen de este artículo), y en el otro fichero Excel tenéis la calculadora de la TAE.

Calcular la TIR de una inversión, para periodos irregulares

Cuando calculamos la TIR de una inversión, lo normal es que los flujos de caja estén todos referidos a unos mismos periodos de tiempo, es decir, que todos los momentos donde se producen los flujos guardan siempre la misma periodicidad. Por ejemplo, cuando calculamos la TIR de una inversión, lo normal es que los flujos sean siempre iguales, y si se trata de años, los flujos serán anuales, si se trata de meses, los flujos serán, y así sucesivamente.

En el ejemplo siguiente podéis ver que hay una serie de periodos, y una serie de flujos. El primer periodo, corresponde al momento cero, es decir, al momento actual, o momento presente, y corresponde al desembolso inicial (como es la inversión inicial, es decir, un pago, debemos ponerlo en negativo, para distinguirlo de los cobros periódicos que recibiremos). Podemos ver que no nos interesan los periodos de tiempo (no sabemos a la vista de ese pantallazo, si se trata de meses, años, semestres, o cualquier otro periodo), porque se da por hecho que son todos iguales. En la fórmula que podéis ver en el pantallazo siguiente, podéis observar que hemos puesto un 5% como tipo de interés estimado, a partir del cual Excel obtendrá la TIR correcta, aunque si se omite, Excel parte de un tipo de interés del 10%, como interés inicial a partir del cual hará las estimaciones. La TIR obtenida es del 6,7075%, pero no decimos si se trata de una TIR anual, semestral, mensual, etc. ¿Por qué no lo decimos?. Pues porque esa TIR estará expresada en función del periodo. Es decir, si esos periodos 0, 1, 2, 3, 4, 5, y 6, son meses, es decir, pagos y cobros mensuales, la TIR será mensual, y si se trata de años (como es lo más habitual), pues la TIR será anual:


Suponiendo que estamos hablando de la TIR anual, la imagen anterior, podemos hacerla más legible, de la siguiente forma, donde hemos añadido las fechas. Aparte, podéis observar que en la fórmula de la TIR, hemos omitido el tipo de interés inicial a partir del cual Excel hará la estimación de la TIR:


Todo esto, junto con el cálculo del valor actual neto, ya lo habíamos explicado en un artículo donde precisamente hablábamos de cómo calcular la TIR y el VAN. También habíamos visto como calcular la TIR con Solver (una potente herramienta de Excel, para optimización).

Ahora la cuestión es la siguiente: ¿Qué pasaría si en lugar de tener los periodos uniformes, se tratase de periodos con diferente periodicidad?. Vamos a suponer que en lugar de recibir esos flujos de cada el día 10 de cada año (ver imagen anterior), se reciben en las siguientes fechas:


¿Sería correcto utilizar la función TIR, para evaluar la tasa interna de rentabilidad de esta inversión, teniendo en cuenta que los periodos no son homogéneos?. Efectivamente, no. Para ello, deberemos utilizar la función TIR.NO.PER, de la siguiente forma:

=TIR.NO.PER(flujos de caja; fechas; tipo de interés estimado)

Como ocurre con la función TIR, podemos omitir el último argumento, donde se nos solitita el tipo de interés a partir del cual Excel hará las estimaciones. Si lo omitimos, Excel presupone que es el 10%.

En nuestro ejemplo anterior, donde hay periodos que no guardan la misma periodicidad, deberemos introducir esta fórmula para calcular la TIR:

=TIR.NO.PER(D6:D12;C6:C12;5%)

El resultado sería que nuestra TIR es de 10,8779%, como podéis ver en la siguiente imagen:


Si os fijáis en los dos ejemplos que ilustran este artículo, veréis que los flujos son los mismos (idénticas cantidades, tanto en pagos como en cobros), pero no son los mismos los periodos donde se producen. Es por ello, que utilizar correctamente las funciones para calcular la TIR, es básico para hacer correctamente las cosas. Solo hay que controlar si los periodos son uniformes o no, para elegir la función TIR o la función TIR.NO.PER.

Calendarios para imprimir

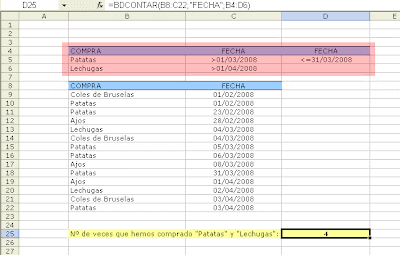
Suele ser habitual que cuando finaliza un año, mucha gente empieza a planificar sus proyectos para el año siguiente: dejar de fumar, apuntarse al gimnasio, hacer dieta, viajar fuera del país, etc. Seguramente, muchos de los afortunados que tenemos empleo, lo primero que hacemos es buscar un calendario para mirar en qué días cae la Semana Santa, miramos también las vacaciones de verano, los días de Navidad, fin de año, y algún que otro puente, porque lo que más deseamos es disfrutar esos días, desconectando alejados de la fábrica o de la oficina.

Lo normal es que no dispongamos de un calendario del año que viene, hasta unos pocos días antes de la llegada del nuevo año, bien porque nos manda una agenda un proveedor, bien porque nos regala un calendario de pared una entidad financiera, o bien porque nos lo manda una empresa que no conocemos y que quiere vendernos algún producto o servicio.

Pues bien, hoy vamos a ver como podemos generar nuestros propios calendarios para imprimir y poder tenerlos siempre a mano, para cuando los necesitemos. Para ello utilizaremos Excel, esa potente herramienta que nos permite tratar no solo datos numéricos, o de texto, sino también fechas y unidades de tiempo. Excel tiene una limitación en cuanto al tratamiento de fechas, que hace que solo podamos operar con ellas, si están comprendidas entre el 01-01-1900 y el 31-12-9999. En el caso de utilizar Excel en su versión para un ordenador Macintosh, el rango de fechas permitidas, pasa a ser desde el 01-01-1904, hasta el 31-12-9999.

Nosotros vamos a generar un calendario para imprimir que cubra el rango desde el año 1920 hasta el 2100. ¿Parece suficiente, verdad?. Pues bueno, si todavía quieres más años, simplemente cambiando una línea del código fuente, podrás alterar ese rango, por si deseas acomodarlo adaptándolo completamente las posibilidades de Excel (si usas una versión para PC, desde el año 1900 al 9999, y si utilizas Excel para Mac, desde el año 1904 al 9999).

Lo primero que haremos será crear los 12 cuadros, cada uno para cada mes. Cada cuadro estará formado por una celda combinada, donde incluiremos el nombre del mes, y 49 celdas de 7x7, para los días de la semana.


Lo que haremos, será solicitar vía un InputBox, el año para el cual queremos crear el calendario. Una vez introducido, se nos generarán los días de cada mes, colocándose donde les corresponde. Si el día 1 de enero cae en martes, pues aparecerá él martes, y si cae en viernes, pues aparecerá en viernes. Para hacer todo esto, utilizaremos exclusivamente funciones de Excel. Concretamente, para el nombre del mes, tomaremos como referencia el año, que está en la celda K2. En el caso concreto del mes de enero, por ejemplo, la función será esta:

=FECHA($K$2;1;1)

Para la primera fila, y en el caso del mes de enero, bajo el rótulo lunes pondremos esta fórmula:

=SI(ELEGIR(DIASEM(B5);"Do";"Lu";"Ma";"Mi";"Ju";"Vi";"Sa")=B6;1;"")

Para el resto de días de la semana, pondremos un condicional. En el caso del martes, utilizaremos por ejemplo, esta:

=SI(B7="";SI(ELEGIR(DIASEM($B$5);"Do";"Lu";"Ma";"Mi";"Ju";"Vi";"Sa")=C6;1;"");B7+1)

En la segunda fila, bajo el lunes, y en el caso de estar trabajando con el mes de enero, pondremos esta fórmula:

=SI(H7<>"";SI(H7+1>DIA(FIN.MES($B$5;0));"";H7+1);"")

Para el resto de días de la semana, haremos algo parecido, cambiando en la fórmula anterior, la celda H7, por la celda inmediatamente anterior al día de la semana con el que estemos trabajando.

El modelo, como veis, no tiene mucha complicación, Tan solo hay que utilizar la fórmula ELEGIR, para saber junto con DIASEM, el día de la semana, y compararlo con los datos que aparecen arriba y que contienen el día de la semana (Lu, Ma, Mi, etc.), aunque podéis utilizar otras fórmulas, para obtener esos mismos resultados. También utilizaremos la función FIN.MES, para saber cual es el último día del mes, y que no siga rellenando el calendario más allá del día 30 o 31 (en el caso de febrero, del 28 o 29, según proceda).

Si la función FIN.MES os devuelve el error #¿NOMBRE?, hay que tener habilitadas las herramientas para análisis. Eso es tan sencillo como marcar la opción Herramientas para análisis, desde el menú Herramientas, y seleccionando a continuación Complementos...

Por otra parte, me comentan, que al abrir el fichero desde una versión de Excel en inglés, la función FIN.MES no la traduce de forma automática. En ese caso hay que hacer un reemplazo (desde Edición, seleccionando la opción Reemplazar), y sustituir FIN.MES por EOMONTH.

Como parece que estar leyendo todo esto, puede parecer un poco lioso, si no tenemos delante el fichero de Excel, lo mejor es que lo descarguéis, y lo probéis. Al final de este artículo, hay un enlace para descargarlo.

Los macros que utilizaremos, son realmente sencillos. El primero será este, que hará que se proteja la hoja, para que nadie cambie ni borre nada. La protección no tiene ningún password:

Sub Auto_open() 'Al abrir el libro, 'protegemos la hoja (sin ningún password) ActiveSheet.Protect End Sub

El segundo macro es para imprimir el calendario, definiendo el área a imprimir, ajustado a las dimensiones de 1 página de alto y 1 de ancho, y encajándolo todo, horizontal y verticalmente:

Sub imprimir_calendario() 'Seleccionamos el área para imprimir ActiveSheet.PageSetup.PrintArea = "$A$1:$Y$40" 'definimos las preferencias de impresión With ActiveSheet.PageSetup 'Centramos la impresión .CenterHorizontally = True .CenterVertically = True 'Ajustamos la impresión a 1 página 'tanto de alto como de ancho .Zoom = False .FitToPagesWide = 1 .FitToPagesTall = 1 End With 'Imprimimos el calendario ActiveWindow.SelectedSheets.PrintOut Copies:=1 End Sub

Este último macro, es para el año. Pondremos el texto en un tamaño de fuente de 18 pixels, lo centraremos en un rango de celdas, y le añadiremos delante el texto "Año", entre otras cosas:

Sub anio() 'Ocultamos el procedimiento Application.ScreenUpdating = False 'Desprotegemos la hoja ActiveSheet.Unprotect 'fichamos la celda donde estamos celda = ActiveCell.Address 'Presentamos un inputbox para preguntar el año respuesta = InputBox("Introduce el año:", "Año") 'Si el año está entre 1950 y 2100, lo escribimos 'en la celda K2, en caso contrario, mostramos un mensaje If Not IsNumeric(respuesta) Or respuesta < 1920 Or respuesta > 2100 Then 'mostramos un mensaje MsgBox ("No es un año válido. Debe estar entre 1920 y 2100") Exit Sub Else 'si el año es válido, lo escribimos en la celda K2 Range("K2").Select ActiveCell = respuesta Selection.NumberFormat = """Año"" ###0" 'ponemos el año en grande, y lo centramos With Selection.Font .Size = 18 End With Range("K2:O2").Select With Selection .HorizontalAlignment = xlCenter End With Selection.Merge End If 'volvemos donde estábamos Range(celda).Select 'protegemos la hoja ActiveSheet.Protect 'Mostramos el procedimiento Application.ScreenUpdating = True End Sub

Por cierto, a este último macro, le he puesto por nombre “anio” en lugar de “año”, por si algún usuario no tiene en su teclado la letra ñ, o por si usa una versión inglesa de Excel, y para evitar posibles problemas al convertir las funciones y los procedimientos.

Si deseáis añadir el complemento de las herramientas para análisis directamente a través de un macro, podéis añadir esta primera línea al macro Auto_open():

AddIns("Herramientas para análisis").Installed = True

Aquí podéis ver un pantallazo de cómo nos quedaría el calendario, una vez elegido el año. Evidentemente esto no será lo que saldrá por la impresora cuando imprimamos el calendario, pues se trata de un pantallazo para ilustrar este artículo, y aquí salen visibles los botones para los macros:


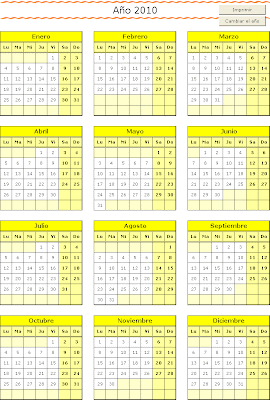
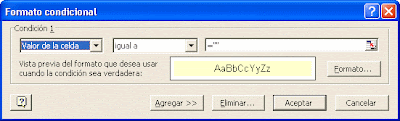
Para los más curiosos, en el calendario se utiliza también el formato condicional, con el fin de poner de color amarillo suave, aquellas celdas que no contienen ningún día, y diferenciarlas así, de aquellas que tienen un número. Si nos situamos en cualquier celda, y vamos a la opción de menú Formato, y a continuación a Formato condicional…, veremos esto (aunque no se pueda apreciar muy bien, aparece en color amarillo pálido, el fondo de la celda):


Si preferís utilizar calendarios con más decoración, con imágenes, y que no estén hechos en Excel, sino con otras aplicaciones, podéis pasaros por algunos sitios de la red. Entre otros, podéis visitar por ejemplo, este blog que contiene abundante información sobre cómo obtener calendarios para imprimir, aunque posiblemente este último sitio esté dirigido más a un público infantil, al que seguramente Excel todavía les suena a chino :-)

Desde aquí podéis descargar el fichero, con el ejemplo que hemos visto en este artículo, para que podáis elaborar vuestros propios calendarios para imprimir.

Horas de 100 minutos, y conversión de unidades de tiempo

Muchos de los usuarios que llegan a este blog de excel, lo hacen buscando como trabajar con horas de 100 minutos, para que sean interpretadas como horas normales de 60 minutos. La cuestión es bastante sencilla, pues no se trata de algo directamente relacionado con excel, sino con las matemáticas básicas. Desconozco el motivo por el cual muchos usuarios trabajan con horas de 100 minutos. Quizás se trate de datos importados de otras aplicaciones, o de controles horarios especiales, pero da igual el motivo. Como son bastantes las visitas que google manda a este blog, buscando una solución al tratamiento de ese tipo de "horas especiales", he decidido que como se acerca Navidad, tenía que ser un poco condescendiente con estos -seguramente esporádicos- lectores.

Una simple regla de tres, es la solución a ese tipo de problemas. Veámoslo con unos sencillos ejemplos:

Si esos 100 minutos –llamémosles, especiales-, queremos que sean el equivalente a 1 hora, la lógica nos dice que 50 minutos especiales serán el equivalente a media hora. Veámoslo con más ejemplos de este estilo:

100 minutos de tipo "especial" = 1 hora = 60 minutos
50 minutos de tipo "especial" = 1/2 hora = 30 minutos
25 minutos de tipo "especial" = 1/4 de hora = 15 minutos
12,5 minutos de tipo "especial" = 1/8 de hora = 7,5 minutos

Para hacer la conversión correspondiente, nos bastará con utilizar una regla de tres, del siguiente tipo:

100 minutos de tipo "especial" = 60 minutos ME minutos de tipo "especial" = MM minutos

En la regla de tres anterior, ME es el número de minutos especiales que conocemos, y que queremos pasar a su equivalente en minutos convencionales (MM). Podemos convertir esa regla de tres en la siguiente ecuación:

MM = (60 x ME) / 100

Por ejemplo, si tenemos horas de 100 minutos, y queremos obtener el equivalente de 90 minutos -que están expresados en esas horas especiales-, a la cantidad de minutos convencionales, obtendremos esto:

MM = (60 x 90) / 100 = 54 minutos

Así que ya lo sabemos: 90 minutos "especiales", son exactamente 54 minutos "de los de toda la vida" :-)

Aprovechando la situación, otro numeroso grupo de usuarios llega a este blog de excel, buscando como convertir horas minutos, minutos a segundos, horas a segundos, etc. Vamos a usar de nuevo el sentido común, para dar respuesta a estas otras dudas.

Si sabemos que 1 hora son 60 minutos, no será difícil deducir que 2 horas serán 120 minutos. Usando la lógica, podremos montar una tabla como la que sigue:

1 hora = 60 minutos 2 horas = 2 x 60 minutos = 120 minutos 3 horas = 3 x 60 minutos = 180 minutos 4 horas = 4 x 60 minutos = 240 minutos 5 horas = 5 x 60 minutos = 300 minutos Y así podríamos seguir indefinidamente...

La regla que sigue esa tabla, habrás visto que es muy sencilla:

Si queremos pasar X horas a minutos, tan solo deberemos multiplicar el número de horas por 60 minutos:

Pasar de horas a minutos: Nº de minutos = Nº de horas x 60

Podemos hacer lo mismo con el resto de unidades de tiempo. Para pasar de horas a segundos, si sabemos que 1 hora tiene 60 minutos, y 1 minuto tiene 60 segundos, nos bastará con utilizar esta fórmula:

Pasar de horas a segundos: Nº de segundos = Nº de horas x 60 x 60

Pasar de minutos a segundos: Nº de segundos = Nº de minutos x 60

Pasar de minutos a horas: Nº de horas = Nº de minutos / 60

Pasar de segundos a horas: Nº de horas = Nº de segundos / 60 / 60

Pasar de segundos a minutos: Nº de minutos = Nº de segundos / 60

Es importante destacar que el dato que obtendremos en todas estas conversiones de unidades de tiempo, serán números decimales, y no fracciones de unidades de tiempo. Por ejemplo, si estamos convirtiendo 150 minutos a horas, si aplicamos la fórmula correspondiente, tendremos que dividir 150 entre 60, con lo que obtendremos 2,5 horas. Esta cifra no indica que se trata de 2 horas y 50 minutos (ni tampoco 2 horas y 5 minutos), pues esa cifra no es una fracción de tiempo, sino una fracción decimal, por eso debe interpretarse como 2 horas y media (2’5 horas).

Convertir unidades de tiempo a formato hh:mm:ss

El otro día me preguntaba un lector del blog, como podía convertir por ejemplo 66 minutos, en formato horario, del tipo 1:06, y le contesté en otro comentario de este blog. Le contesté, complicándome la vida, porque a pesar de haberle dado una respuesta correcta, le dí la respuesta más complicada, ya que la propuesta que le sugerí incluía una larga fórmula.

Luego me acordé que en otro artículo de este blog, ya hablaba algo parecido. Concretamente cómo trabajar con horas, minutos, y segundos, y como controlar diferencias horarias, o como pasar de formato horario a decimal (y por lógica, sabiendo eso, también podemos pasar de formato decimal, a formato horario), por ejemplo. En otro artículo profundizaba sobre aluno de estos temas, y hablaba específicamente sobre como convertir unidades horarias, a formato decimal (por ejemplo, como pasar 7:30 h. a su valor decimal, que es 7,5).

El artículo del primer enlace, más la consulta de ese usuario que os mencionaba al principio, me han llevado a escribir este artículo donde explico como convertir una cantidad horaria (ya seas segundos, minutos, u horas), a su formato hh:mm:ss, de una forma muy sencilla, sin necesidad de aplicar fórmulas complicadas.

Aquí os dejo un pantallazo, para que os hagáis idea de lo que quiero transmitiros:


Si por ejemplo tenemos en la celda C7 un número de horas determinadas, y queremos pasarlas a formato hh:mm:ss, tan solo tendremos que aplicar ese formato de celda, a la celda donde queremos mostrar el resultado, y además, aplicar esta sencilla fórmula:

=C7/24

Si tenemos en la celda C8 un número de minutos determinados, y queremos pasarlos a formato hh:mm:ss, tan solo tendremos que aplicar ese formato de celda, a la celda donde queremos mostrar el resultado, y además, aplicar esta sencilla fórmula:

=C8/24/60

Si tenemos en la celda C9 un número de segundos determinados, y queremos pasarlos a formato hh:mm:ss, tan solo tendremos que aplicar ese formato de celda, a la celda donde queremos mostrar el resultado, y además, aplicar esta sencilla fórmula:

=C9/24/60/60

Para una cantidad de segundos, minutos, u horas, que sean igual o superior a las 24 horas, se computará un nuevo ciclo horario, como si se tratase de un nuevo día (partiendo de cero), por lo que el resultado no tendrá en cuenta los segundos, minutos, días acumulados con anterioridad. Por eso, que si trabajamos con horas que sean iguales o superiores al ciclo horario del día (24 h), los resultados que obtengamos pueden no ser correctos. En un comentario de este blog -no recuerdo si era en alguno de los dos artículos cuyos links que incluía al principio–, y en respuesta a otra pregunta que me hacía un usuario del blog sobre como trabajar con unidades de tiempo superiores a las 24 h., le daba una opción para solventar ese problema.

Desde aquí podéis descargar el fichero de excel, con el ejemplo que os presento en este artículo. Esta hoja de cálculo está protegida, para que solo podáis cambiar los datos de tres celdas, pero no tiene password, así que con un simple "intro" basta para desprotegerla, desde Herramientas, Proteger, Desproteger hoja….

Calcular el umbral de rentabilidad, con Excel

Con el umbral de rentabilidad, inicio una serie de artículos, que de manera no periódica iré publicando, referidos específicamente a temas de gestión empresarial, y cómo solventarlos o como resolverlos, aplicando una sencillas fórmulas, funciones (o macros, si llegara el caso), con nuestra estupenda hoja de cálculo excel.

Sin entrar en analizar de forma exhaustiva, el concepto de umbral de rentabilidad (o también llamado, punto muerto), intentaré sintetizarlo, definiéndolo como el volumen de ventas, a partir del cual la empresa empieza a generar beneficios. Cuando una empresa vende 0 (cero) unidades, está perdiendo dinero, cuando vende 10 unidades de su producto, es muy probable que siga perdiendo dinero, y si vende 50.000 unidades, es probable que esté empezando a ganar dinero. El umbral de rentabilidad, nos determina el volumen de ventas donde la empresa obtiene un beneficio cero, es decir, es el punto exacto a partir del cual la empresa entra en beneficios (gana dinero).

Vamos a ilustrar el concepto de umbral de rentabilidad o punto muerto, con un gráfico, donde la línea azul indica el volumen de ingresos, al aumentar las ventas, y la línea roja, el volumen de gastos totales, al aumentar también las ventas.


Con excel, podemos determinar esta cifra de ventas de una forma muy sencilla. Antes de entrar en ello, cogeremos el concepto económico del umbral de rentabilidad, y lo analizaremos matemáticamente. Para ello, explicaremos antes el significado de una serie de variables que necesitaremos:

I = ingresos
C = cantidad vendida
p = precio de venta unitario (precio de cada unidad C)
G = gastos totales
GF = gastos fijos
GV = gastos variables
gv = gastos variables unitarios (gastos variables de cada unidad C)
R = resultado (beneficio o pérdida de la empresa)

Los costes variables son aquellos que varían, al cambiar la referencia sobre la que son estudiados. Normalmente, esta referencia, es el volumen de producción (o también el volumen de ventas), por lo que los costes variables son aquellos que varían al cambiar (aumentar o disminuir) la cantidad producida (o la cantidad vendida). En una empresa que vende productos, el coste de las materias primas es el coste variable más importante, aunque hay muchos más. Los costes fijos, son aquellos que permanecen invariables al variar la cantidad producida. Un ejemplo de coste fijo, es el coste de personal, pues el coste fijo de fabricar 10 unidades, será el mismo que el de fabricar 15 unidades, ya que el coste de personal, es un coste fijo sin dependencia directa respecto del volumen de producción (excepto por la parte del coste de las horas extras, que se consideraría un coste variable). En el ámbito interno de la empresa, los gastos fijos y los gastos variables, suelen denominarse costes fijos y costes variables.

Una vez definidas esas variables, entraremos a formular matemáticamente el concepto, antes de programar nuestra hoja de cálculo excel.

Sabemos que el resultado de una empresa, es la diferencia entre sus ingresos y sus gastos, por tanto:

R = I - G

Sabemos también que los ingresos, son igual a la cantidad vendida, por el precio de cada unidad:

I = C · p

Y que los gastos totales son la suma de los gastos fijos, más los gastos variables:

G = GF + GV

Los gastos variables son igual a la cantidad vendida, multiplicada por el coste variable de cada unidad:

GV = C · gv

Entonces, podemos sustituir todo eso, en la ecuación inicial, R = I - G:

R = (C · p) - (GF + (C · gv))

O lo que es lo mismo:

R = (C · p) - GF - (C · gv)

Como en el umbral de rentabilidad, el resultado es cero, entonces sustituimos R, por 0:

0 = (C · p) - GF - (C · gv)

Pasamos GF al lado izquierdo de la ecuación:

GF = (C · p) - (C · gv)

O lo que es lo mismo:

GF = C · (p - gv)

Es decir:

GF / (p - gv) = C

Ya tenemos la fórmula que nos determina, a partir de qué cantidad de unidades vendidas, empezaremos a tener beneficios. Cambiando los términos de la ecuación de lado, esta es la fórmula:

C = GF / (p - gv)

Como veis, el umbral de rentabilidad es un concepto económico muy sencillo, pero de gran utilidad, pues nos sirve para determinar el volumen de ventas que debe tener la empresa, para poder entrar en beneficios. Si sabemos que en el umbral de rentabilidad el resultado es cero, vendiendo una unidad más, la empresa entrará en beneficios, pues los ingresos son mayores que los gastos, como podéis ver en el gráfico anterior, mientras que vendiendo una unidad menos, la empresa estaría todavía en pérdidas, pues los gastos son mayores que los ingresos, como podéis ver también en el gráfico anterior.

He aquí un ejemplo de cálculo del umbral de rentabilidad, para el caso de una empresa que fabrica tres productos diferentes. He sintetizado mucho los conceptos, para que sea más inteligible, pero en la vida real, no te encontrarás con una partida de gastos fijos, así, sin detalle, sino todo lo contrario, te encontrarás con múltiples gastos de carácter fijo, que sumándolos, te permitirán obtener el total de los gastos fijos, y que será la cifra que necesitaremos. Puedes ampliar la imagen adjunta donde se muestra una tabla de excel con los resultados de nuestros cálculos, haciendo clic sobre ella:


Desde aquí podéis descargar el fichero de excel, con el ejemplo que os presento en este artículo.

Control horario: Horas normales y horas extras

Sois muchos los que llegáis a este blog buscando una solución que os permita controlar la hora de entrada y salida de los empleados de la empresa. En concreto, muchos usuarios buscan una hoja de cálculo que les permita obtener tanto el número de horas normales de la jornada laboral (horas ordinarias), como el número de horas extras. Pues bien, atendiendo a estas solicitudes, he preparado una hoja de cálculo, que podréis descargar al final de este artículo, y que servirá de ejemplo. Espero que esta hoja de cálculo cubra todas nuestras necesidades, a la hora de calcular jornadas laborales ordinarias, horas extras, y remuneraciones por horas extraordinarias.

La hoja de cálculo no contiene macros, sólo contiene fórmulas de excel, y además no son nada complejas. Quizás algunas de las fórmulas sean un poquito farragosas, y requieran algo de tiempo para interpretarlas, pero una vez asimiladas, veréis que el tema no era tan complejo. Fijaos bien en el formato que tienen las celdas. Algunas de ellas tienen formato de fecha, numérico, y otras formato personalizado.

En esta hoja de cálculo, tenemos una serie de datos de entrada:

En la celda D4 introduciremos la hora de entrada.
En la celda D5, haremos lo mismo pero con la hora de salida.
En la celda D6 introduciremos el número de horas dedicadas a comer.
En la celda D7, y con una simple fórmula, obtendremos la jornada laboral ordinaria (sin contar horas extras). Si introdujéramos un dato manualmente, en esta celda D7, y fuera un dato inconsistente, en la celda D8 nos aparecería un mensaje informándonos que el número de horas ordinarias no es correcto.
En la celda D10, introduciremos el nombre del empleado.
En la celda D11, informaremos el precio de la hora extra, ya sea bruto, o neto. Dependiendo de si hemos introducido el importe bruto, o neto, la cifra total obtenida por las horas extras trabajadas, evidentemente atenderá también a ese mismo criterio, bruto o neto.

En esta hoja de cálculo, podemos observar también varias columnas:

La columna B y C, corresponden a la fecha y hora de entrada del empleado. Deberemos informar de ello diariamente, bien introduciendo el dato manualmente, o importándolo a través de algún otro programa (con un macro podríamos automatizar esta tarea).
La columna D y E, corresponden a la fecha y hora de salida del empleado. Deberemos informar también introduciendo el dato manualmente, o importándolo a través de algún otro programa.
La columna F nos informa de la cantidad de horas normales (horas dentro de la jornada laboral ordinaria), y es una fórmula.
La columna G nos informa de la cantidad de horas extraordinarias (las horas que exceden del horario laboral normal), y es una fórmula.
La columna H nos informa de las horas totales trabajadas (suma de horas normales, más horas extras). Se trata de una simple fórmula que suma las dos columnas anteriores.
La columna I nos informa de las horas y fracciones, en números decimales (ya sabes que por ejemplo 7:30, es decir, siete horas y treinta minutos, son en números decimales 7,5 horas). Nos bastará con multiplicar la columna inmediatamente anterior, por 24 (aunque también le hemos añadido la coletilla " h." en el formato de la celda).
La columna J nos informa del coste de las horas extraordinarias, siempre y cuando hayamos informado del precio por hora, en la celda D23. En la celda E23 informaremos de la moneda (en nuestro ejemplo, euros). Dependiendo del tipo de moneda elegido, la columna J nos mostrará el importe de las horas extras, expresado en la moneda elegida. La columna J nos muestra las cifras en formato texto, así que no intentéis sumar los datos de la columna, porque no obtendréis ningún resultado. Si deseáis que los importes siempre sean tratados como números, tan solo tendríais que multiplicar la columna F de las horas extras, por el coste de cada hora extra, que es el que figura en la celda D11.

Finalmente, en la celda E25 tendríamos el número de horas que el empleado no ha justificado, es decir, el número de horas que el empleado ha faltado (se ha ausentado), dentro del horario laboral normal de la empresa. Esta cifra la obtendremos comparando las horas de la columna F, con el número de horas ordinarias que aparece en la celda D7.

Aquí os dejo un pantallazo de la hoja de cálculo. Si deseáis ver la imagen más grande, tan solo tenéis que cliquear sobre de ella:


Desde aquí podéis descargar el fichero de excel, con el ejemplo que os presento en este artículo.

Uso de la función BDContar

Aprovechando que ayer Neus, una lectora del blog que dejó una pregunta sobre como operar con fechas, y como agrupar datos, os pongo aquí la solución.

Se trata de una hoja de cálculo donde tenemos una serie de productos que hemos comprado en diferentes días. Un día hemos comprado lechugas, otro patatas, al siguiente lechugas, y al otro coles de Bruselas. Se trataría de determinar cuantas veces a lo largo de un periodo de tiempo, hemos adquirido tal o cual producto.

Los datos serían estos:


Y queremos determinar cuántas veces hemos comprado patatas entre el 1 y el 31 de marzo de 2008.

Una de las formas más sencillas de solucionarlo (seguramente habrá alguna otra más compleja, pero no he entrado a analizar esa posibilidad), es utilizando la función de bases de datos llamada BDContar. Ya sabemos todos que Excel no es la aplicación de Office más apropiada para gestionar grandes volúmenes de información con datos uniformes, y que Access sería la aplicación más indicada, pero para pequeños volúmenes de información, Excel nos es más que suficiente.

Pues bien, este sería el planteamiento con Excel. Fijaos en la zona sombreada en rojo:


Esa zona sombreada en rojo, es el sitio donde hemos incluido las condiciones a evaluar en la fórmula. La fórmula es esta:

=BDCONTAR(B8:C22;"FECHA";B4:D5)

Donde el rango de datos que hay entre B8 y C22 es la tabla con los productos y las fechas, el rango que va desde B4 hasta D5, es el rango de condiciones, y FECHA es el campo cuyas condiciones queremos evaluar.

Si por ejemplo quisiéramos evaluar cuantas veces se han comprado patatas entre el 1 y el 31 de marzo de 2008, y cuantas veces se han comprado lechugas a partir del 1 de abril, deberíamos incluir esto:


Y la fórmula sería ahora esta otra:

=BDCONTAR(B8:C22;"FECHA";B4:D6)

Desde aquí podéis descargar el fichero de excel, con el ejercicio resuelto.

Tiempo transcurrido entre dos fechas

En el siguiente ejemplo, vamos a calcular el tiempo transcurrido entre dos fechas, evaluando los años, meses, y días transcurridos. Una de esas fechas, supondremos que corresponde a la fecha de hoy. La otra fecha será la fecha de nacimiento de una serie de personas. Vamos a calcular el tiempo transcurrido desde el día de su nacimiento, hasta hoy.

Para ello, fijaos en esta imagen (doble clic para ampliarla, si no veis bien los detalles):


Antes de nada, comentaros que el texto "años", "meses", y "días", que se muestra en las celdas C5, D5 y E5 lo podríamos haber puesto de muchas formas distintas, pero he optado por hacerlo dándole formato a las celdas, desde Formato, Celdas…, y en la pestaña Número, dentro de la categoría Personalizada, poniendo para el caso de C5, esto que aparece en la imagen (en el caso de D5 y E5 será similar, pero poniendo texto "meses", "días", y "años"):


Si os fijáis, en la celda C5 de la primera imagen, es donde evaluamos los años transcurridos. Tenemos esta fórmula:

=SIFECHA(B5;C$2;"y")

El símbolo del $ nos indica que estamos trabajando con una referencia absoluta, así podremos copiar esa fórmula de C5 en las celdas que hay por debajo, sin necesidad de tener que cambiar ningún dato de la misma. Pues bien, si os fijáis, estamos utilizando la función SIFECHA, que consta de tres partes. La primera de ellas corresponde a la fecha final (la fecha más actual), la segunda corresponde a la fecha inicial (la fecha más antigua), y la tercera parte, la más importante, corresponde al periodo a evaluar, en este caso los años transcurridos (en números enteros), por eso utilizamos "y" (y = years, es decir, años). Es decir, esa fórmula nos está informando del número de años enteros que han transcurrido entre esas dos fechas.

En la celda D5, donde evaluamos los meses transcurridos, tenemos algo parecido:

=SIFECHA(B5;C$2;"ym")

Si os fijáis, esta fórmula, se diferencia de la anterior en el tercer término, donde ahora aparece "ym". Esta parte nos viene a decir que queremos mostrar los meses (también en números enteros) m (m = months, es decir, meses) que pasen de los años enteros y. Si en lugar de poner en ese tercer término ym, hubiésemos puesto m, habríamos obtenido 478 meses, en lugar de 10. La razón es muy sencilla: con m obtenemos los meses transcurridos desde esas dos fechas (la inicial y la final), mientras que con ym solo obtenemos aquellos meses que han transcurrido desde el último año entero (en este caso, 39), y que todavía no llegan para formar otro año, es decir, no llegan a 12 meses.

En la celda E5, tenemos esta función, donde evaluaremos los días transcurridos:

=SIFECHA(B5;C$2;"md")

En este caso, el md del tercer término nos informa de que queremos obtener los días que hayan transcurrido desde el último mes entero. Como en el ejemplo de E5, no llegamos a obtener 11 meses (son 10 meses y pico como véis en la tabla, y precisamente lo que deseamos obtener ese "pico"). Si hubiésemos puesto d, en lugar de md, habríamos obtenido 14.562 días, en lugar de los 13 días que hemos obtenido. La razón es similar al caso anterior de los meses. Utilizando d (d = days, es decir, días), estamos obteniendo la diferencia en días entre la fecha inicial y final. Con md solo mostramos los días d que han transcurrido desde el último mes entero m (desde el mes 10, en adelante).

Si deseamos unir esos tres datos, en una sola celda, podemos concatenarlos (unirlos) con el operador &, al que le añadiremos entre comillas, un texto que informará de si son años, meses, o días. Por ejemplo, en F5 tenemos esta fórmula (debéis ponerla toda en una línea, aunque yo la he puesto en dos para que no se descoloque en pantalla):

=SIFECHA(B5;C$2;"y") & " años " & SIFECHA(B5;C$2;"ym") & " meses " & SIFECHA(B5;C$2;"md") & " días"

Para calcular la diferencia entre dos fechas, podemos utilizar las siguientes opciones:

=SIFECHA(fecha_final;fecha_inicial;"y") =SIFECHA(fecha_final;fecha_inicial;"m") =SIFECHA(fecha_final;fecha_inicial;"d") =SIFECHA(fecha_final;fecha_inicial;"ym") =SIFECHA(fecha_final;fecha_inicial;"yd") =SIFECHA(fecha_final;fecha_inicial;"md")

Cuando en el tercer término utilizamos dos elementos, siempre el primero de ellos debe ser mayor que el segundo, de ahí que pongamos ym, yd, o md. Si utilizamos dm, my, dy, nos dará error por motivos obvios (de igual forma que solo podemos meter un recipiente pequeño en uno grande, y no al revés). En el caso de utilizar ym, estaremos obteniendo el número de días que hayan transcurrido desde el último año entero. Siempre obtendremos por tanto, 364 días (o 365, si estamos hablando de un año bisiesto) como máximo, ya que en cuanto pasemos 1 día de esas dos cifras, ya tendremos un nuevo año entero.

Desde aquí podéis descargar el fichero de Excel, con el ejemplo que hemos visto en este artículo.